Открытый урок

ГЕОМЕТРИЯ . 8 класс.

Урок № 25.

Тема урока: ТЕОРЕМА ПИФАГОРА.

Цель урока: Рассмотреть теорему Пифагора и показать ее применение в ходе решения задач.

Структура урока:

1. Организационный момент.(2 мин.)

2. Актуализация знаний учащихся.(10мин.)

3. Изучение нового материала (10 мин.)

4. Закрепление изученного.(15 мин.)

5. Подведение итогов урока.(5 мин.)

6. Домашнее задание.(3 мин.)

Ход урока:

I.Организационный момент. Сообщить тему урока, сформулировать цели урока.

II.Деловая игра « СТРОИТЕЛЬ». Проверка усвоения учащимися формул для вычисления площадей параллелограмма, треугольника, трапеции и применение полученных знаний к решению практических задач. Ориентация учащихся на профессию строителя.

I этап

Строительное производство сегодня — это механизированный процесс сборки зданий и сооружений из крупноразмерных деталей, изготовленных заводским способом. Столяр работает в строительно-монтажных организациях, на деревообрабатывающих предприятиях, в столярных мастерских. Он выполняет различные операции на станках: на круглопильных — раскрой пиломатериалов, на фуговальных — строгание, на долбежных и шипорезных — выдалбливание гнезд и нарезание шипов у заготовок.

Непосредственно на строительном объекте столяр устанавливает оконные и дверные блоки, производит настилку дощатых и паркетных полов, монтирует встроенную мебель и т. д. Выполнение такой работы невозможно без знания устройства и правил эксплуатации деревообрабатывающих станков, знания технологии и организации строительного производства, умения читать чертежи. Профессия требует объемного воображения, хорошего глазомера, знания геометрии, рисования, черчения.

Постановка задачи. Учитель объявляет, что сегодня все ученики будут выступать в роли строителей. Требуется выполнить работу по настилке полов строящегося детского сада. Предлагается произвести настилку паркетного пола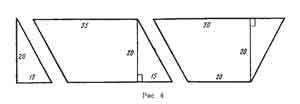 в игровом зале размером 5,75X8 м. Паркетные плитки имеют форму прямоугольных треугольников, параллелограммов и равнобочных трапеций. Размеры плиток в сантиметрах указаны на рисунке 4.

Правила игры. Учащиеся разбиваются на три бригады. Избираются бригадиры.

Первая бригада — столяры. Им нужно изготовить паркетные плитки указанных размеров в таком количестве, чтобы после настилки пола не осталось лишних плиток и число треугольных плиток было минимальным, а плиток в форме параллелограммов и трапеций — одинаковое количество.

Вторая бригада — поставщики. Им нужно доставить необходимое количество плиток на строительную площадку. Они рассчитывают это количество.

Третья бригада — паркетчики. Чтобы проконтролировать доставку, надо наперед знать, сколько и каких паркетных плиток понадобится для покрытия пола.

Побеждает в игре та команда, которая первой выполнит правильный расчет. Для этого надо знать формулы для вычисления площадей вышеуказанных фигур. Учитель записывает на доске, какой материал следует изучить. Учащиеся приступают к работе с учебником. Внутри каждой команды разрешаются взаимоконсультации. При необходимости консультацию дает учитель.

После того как теоретический материал изучен, а формулы для вычисления площадей параллелограмма, треугольника и трапеции записаны в тетрадях, учитель проецирует на доску рисунки и формулы по проработанному материалу. Проводится проверка готовности бригад. С этой целью каждой команде предлагается по два-три вопроса. Ответы учащихся оцениваются очками. Счет записывается на доске.

II этап. Каждая команда приступает к практическим вычислениям. Паркет укладывается в ряды так, что параллелограммы и трапеции чередуются, а треугольников в одном ряду всего два. Подсчеты показывают, что в одном ряду по ширине укладывается по два треугольника и по восемь параллелограммов и трапеций.

Действительно, площадь одной полосы шириной 20 см и длиной 575 см будет 11500 см². Если площадь двух треугольников 300 см², а площадь параллелограмма или трапеции 700 см², то в одной полосе по ширине игрового зала поместится по 8 параллелограммов и трапеций: (11500 —300):700=16. Таких полос в длине комнаты поместится 800:20 = 40. Следовательно, для настилки пола понадобится 80 треугольников и по 320 параллелограммов и трапеций. Проверкой устанавливается: площадь игрового зала 575 X 800 = 460 000 см, площадь одной полосы 575 X 20=11500 см², а таких полос 40, поэтому 11500X40 = 460 000 см² — площадь паркетного пола.

Это самый ответственный этап игры. Вычисляются площади плоских фигур, производятся расчеты.

В конце второго этапа игры учащиеся из каждой бригады дают объяснения около стола учителя, как они вычислили нужное количество паркетных плиток.

Идет разговор об экономии материала.

На первый план выступает математическое содержание работы. Происходит процесс применения знаний на практике.

III. Изучение нового материала.

История открытия теоремы Пифагора.

Полагают, что жил Пифагор около 580—500 гг. до н. э., о жизни его до нас дошли очень скудные данные. По отрывочным сведениям некоторых историков известно, что Пифагор родился на острове Самосе.

В молодости для изучения наук жрецов путешествовал по Египту, жил также в Вавилоне, где имел возможность в течение 12 лет изучать астрологию и астрономию у халдейских жрецов. После Вавилона, побыв некоторое время в своем отечестве, переселился в Южную Италию, а потом в Сицилию и организовал там пифагорейскую школу, которая внесла ценный вклад в развитие математики и астрономии. Однако, приняв количественное отношение за сущность вещей и оторвав их от материального мира, эта школа пришла к идеализму. В политической жизни пифагорейская школа стала реакционной политической организацией рабовладельческой аристократии того времени.

Пифагор и его ученики много потрудились над тем, чтобы придать геометрии научный характер.

Кроме знаменитой теоремы, носящей его имя, Пифагору приписывается еще ряд замечательных открытий, в том числе:

Теорема о сумме внутренних углов треугольника.

2. Задача о покрытии, т. е. деление плоскости на правильные многоугольники (равносторонние треугольники,

квадраты и правильные шестиугольники).

3. Геометрические способы решения квадратных уравнений.

4. Правила решать задачу: «По данным двум фигурам построить третью, которая была бы равна одной из данных и подобна другой».

Наибольшую славу Пифагору принесла открытая им «теорема Пифагора», которая и до настоящего времени считается одной из важных теорем геометрии, используемых на каждом шагу при изучении геометрических вопросов. Частные случаи этой теоремы были известны некоторым народам еще до Пифагора. Например, в своей строительной практике египтяне пользовались так называемым «египетским треугольником» со сторонами 3, 4 и 5. Египтяне знали, что указанный треугольник является прямоугольным, что для него выполняются соотношения 3²+4² = 5², т. е. как раз то, что утверждает теорема Пифагора.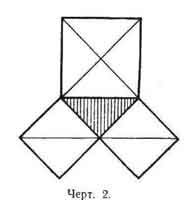

Независимо от Пифагора частные случаи его теоремы использовались также индийцами, причем последние справедливость теоремы Пифагора в частном случае усматривали непосредственно из чертежа. Доказательство Пифагора до нас не дошло. Известный немецкий историк и математик М. Кантор (1829—1920) полагает, что первоначальное доказательство теоремы Пифагора относилось к частному случаю, т. е. к рассмотрению равнобедренного прямоугольного треугольника, как это делали индийцы, исходя непосредственно из чертежа (черт. 2).

В настоящее время имеется свыше ста различных доказательств теоремы Пифагора. Вполне возможно, что среди этих доказательств имеется доказательство и самого Пифагора, если он таким располагал. (Есть мнение, что теорему Пифагора открыл не сам Пифагор, а его ученики. Дело в том, что по тогдашним обычаям все, что открывалось учениками, приписывалось главе школы — учителю.)

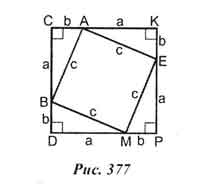
Доказательство теоремы идет под руководством учителя. На доске и в тетрадях

учащихся - рисунок (рис. 377) и доказательство.

Дано: ∆;АВС, С = 90°, АВ = с, ВС = а, АС = Ь.

Доказать: с =а² + Ь².

Доказательство:

а) Достроим ∆АВС до квадрата CKPD со стороной (а + Ь);
Sckpd = (а + Ь) ² = а² + 2 ab + b².

б) ∆ BCA = ∆AKE = ∆ EPM = ∆MDB по двум катетам.

Sbcaa = S_ake=S_epm =S_mdb = ab/2.

в) ВАЕМ- квадрат, S _BAEM = с².

г ) S_ckpd = S_BAEM+ S_BCA+ S_AKE +S_EPM + S_MDB= c²+ 4 ∙ ab/2=

= c ² +2ab= a²+2ab+ b², откуда с²= а² + b².

IV. Закрепление изученного

Решить устно № 483 (а, б), 484 (а, б).

Работа в рабочих тетрадях: решить задачи № 45,46.

Учащиеся работают самостоятельно, по завершении работы один из учащихся читает решение задачи № 45, остальные учащиеся проверяют свое решение, исправляют ошибки.

Таким же образом проверяется задача № 46.

Решить на доске и в тетрадях задачу № 487.

Задача №487

См. рис. 378.

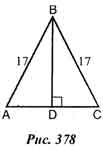
Дано: ∆АВС - равнобедренный, АВ = ВС = 17 см,

АС = 16 см, BD - высота. Найти: BD. Решение:

а) В равнобедренном треугольнике высота, проведенная к основанию, является медианой, поэтому AD = АС : 2 = 16 : 2 = 8 см.

б) ∆ABD - прямоугольный. По теореме Пифагора:

АВ² = AD² + BD², откуда BD² = АВ² - AD² = 17² - 8² = 225. Так как BD > 0, то BD = 15 см.

Наводящие вопросы:

- Сформулируйте свойство высоты, проведенной к основанию равнобедренного треугольника?

- Какая связь существует между сторонами прямоугольного треугольника?

- Как запишется теорема Пифагора для треугольника ABD?

Самостоятельно решить задачи № 485,486 б).

Дополнительные задачи:

1. Большая диагональ прямоугольной трапеции равна 13 см, а большее основание - 12 см. Найдите площадь трапеции, если ее меньшее основание равно 8 см. (Ответ: S_abcd = 50 см².)

2. Основания равнобедренной трапеции равны 10 см и 18 см, а боковая сторона равна 5 см. Найдите площадь трапеции. (Ответ: 42 см².)

V. Подведение итогов урока

Оценить работу учащихся.

Домашнее задание

П. 54, вопрос 8;

Решить задачи № 483 в), г), 484 в), г), д), 486 в);